Qaekwy

Installation

                  Copy
                  pip install qaekwy
python -m qaekwy --version
                  
                

Minimal Example

                  Copy
                  from qaekwy.model.variable.integer import IntegerVariable, IntegerExpressionVariable
from qaekwy.model.constraint.if_then_else import ConstraintIfThenElse
from qaekwy.model.specific import SpecificMaximum, SpecificMinimum
from qaekwy.model.modeller import Modeller
from qaekwy.model.searcher import SearcherType
from qaekwy.engine import DirectEngine

class MinimalExample(Modeller):
    def __init__(self):
        super().__init__()

        # Define integer variables
        self.x = IntegerVariable("x", domain_low=0, domain_high=10)
        self.y = IntegerVariable("y", domain_low=0, domain_high=10)
        self.z = IntegerVariable("z", domain_low=0, domain_high=20)

        # Define an expression variable for the sum of x and y
        self.sum_xy = IntegerExpressionVariable("sum_xy", self.x + self.y)

        self.add_variable(self.x).add_variable(self.y).add_variable(self.z)
        self.add_variable(self.sum_xy)

        # Add constraints
        self.add_constraint(self.sum_xy == 15)  # x + y = 15
        self.add_constraint(self.x == self.y * 2)  # x = 2 * y
        self.add_constraint(
            ConstraintIfThenElse(
                condition=self.x > self.y,
                then_constraint=self.z == self.x + self.y,
                else_constraint=self.z == self.x - self.y
            )
        )  # if x > y then z = x + y else z = x - y

        self.add_objective(
            SpecificMaximum(self.z)  # Maximize z
        )

        self.add_objective(
            SpecificMinimum(self.x)  # Minimize x
        )

        # Set searcher type (e.g., Branch-and-bound)
        self.set_searcher(SearcherType.BAB)

# Initialize the connection to the engine
solver = DirectEngine()

# Send the model and retrieve the solution
solution_response = solver.model(MinimalExample())

# Read and display the solutions, if any
if solution_response and solution_response.get_solutions():
    for sol in solution_response.get_solutions():
        print(f"x: {sol.x}, y: {sol.y}, z: {sol.z}, sum_xy: {sol.sum_xy}")
                

Result

                  Copy
                  x: 10, y: 5, z: 15, sum_xy: 15
                

Modelling & Solving

1. Define a model in Python: variables, domains, constraints, and optional objective.
2. Submit the model to Qaekwy’s engine (cloud-based).
3. The solver searches for solutions that satisfy all constraints.
4. Results are returned as a solution object for inspection in Python.

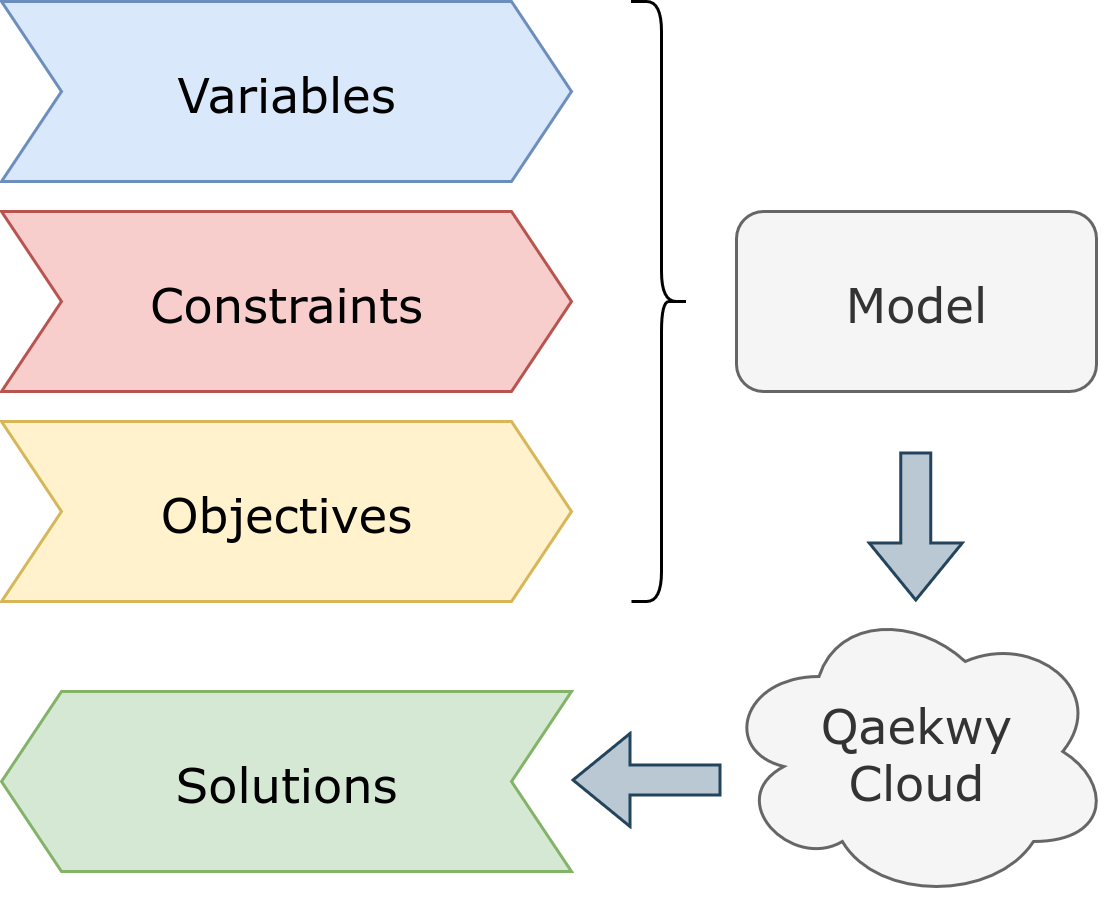
This structure of modelling and solving makes it easy to experiment with strategies and heuristics.

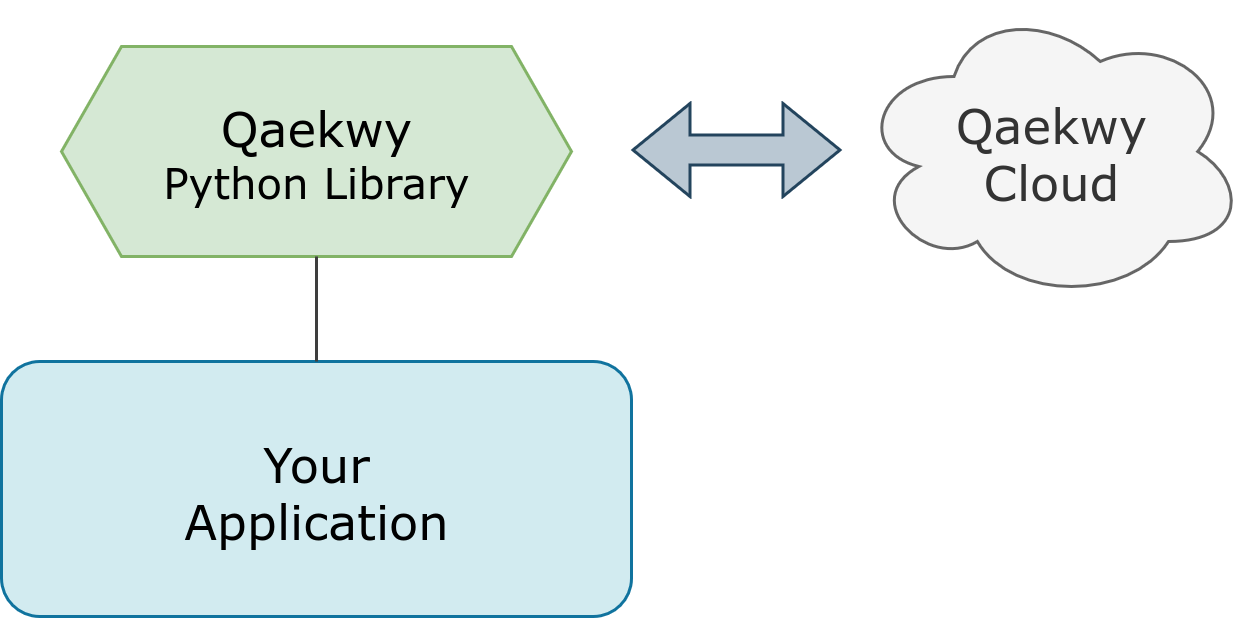
Integration

The model is then sent to the Qaekwy Cloud Engine through REST API. Once a set of solutions has been found, the result is returned.